 |
 |
 |
|
 |
 |
|
 |
 |
|
|
 |
|
|
 |
|
5.4. Triangular tiles. In normal flat tilings it is not required that all the corner points of the tiles meet in one point. In ‘Tilings and Patterns’[1], page 475-481 we can see many examples of polygonal isohedral tilings in which the corner point of one tile touches another tile somewhere at the edge in between two corner points. In Figure 43 such a tiling is shown made by M.C. Escher [4]. This way of connecting the tiles in non-flat tilings can be used also. In the examples (Figure 44 and 45) the constructions are tilings with Glide Rotation. |
|
|
 |
|
|
 |
|
|
 |
|
 |
|
|
|
|
Figure 43: M.C. Escher.
|
Figure 44: Triangular tiles (1).
|
Figure 45: Triangular tiles (2).
|
|
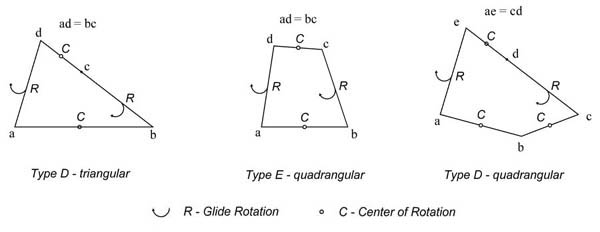
| 5.5. Quadrangular tiles. For convex quadrangular tiles we now have two different ways of using them in non-planar tilings with Glide Rotation as can be seen in Figure 46. In Figure 46 also the triangular tile used in Figures 44 and 45 is shown. |
|
 |
|
|
|
Figure 46: Classification - convex triangular and quadrangular tiles.
|
|
| The use of quadrangular tiles leads to nice constructions. Many variations are possible as can be seen in the examples of Figures 47 to 49. |
|
 |
 |
|
 |
|
 |
|
|
Figure 47: Type E - quadrangular.
|
Figure 48: Type E - quadrangular
|
Figure 49: Type D - quadrangular
|
|
| 5.6. Special cases. Finally I want to show some special cases of the spiral cylinders with quadrangular tiles. For the tile of Type E we can change the shape of the quadrangle in such a way that it becomes a rectangle. And now the top view of the construction shows an equilateral triangle as the shape of the hole. |
|
 |
 |
|
 |
|
|
 |
|
|
 |
|
|
Figure 50: Quadrangular tiles.
|
Figure 51: Rectangular tiles.
|
Figure 52: Rectangular tiles.
|
|
| And when we use a trapezoid with angles 60-60-120-120 degrees we will get a square hole.. |
|
 |
|
 |
 |
|
|
Figure 53: Trapezoids.
|
|
Figure 54: Trapezoids.
|
|
Figure 55: Two entwined spirals.
|
|
| A special case of such a trapezoid is the tile used in the construction of Figure 55. The tile is exactly half of a regular hexagon, and it leads to a non-flat tiling that also can be seen as a combination of two entwined spirals. |
|
| 6.1. Non-flat Tilings. I think the field of non-flat-tilings with flat tiles is interesting and needs further exploration. Especially the use of Glide Rotation leads to interesting new constructions which can be used as designs for sculptures. In other words, it is a topic which can bring art and mathematics together in an elegant way. |
|
|
References
[1] Grünbaum and Sheppard, Tilings and Patterns, W.H. Freeman and Company, New York, 1987.
[2] Luca Pacioli, La Divina Proportione, Edicione Akal, Madrid, 1991 (first published in 1509).
[3] Heesch und Kienzle, Flächenschluss, Spinger-Verlag, Berlin, 1963.
[4] Doris Schattschneider, M.C. Escher: Visions of Symmetry, Harry N. Abrams, 2004 (2nd ed.).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|















