
Figure 1
Figure 2
Figure 3
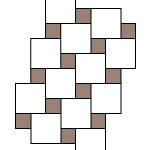
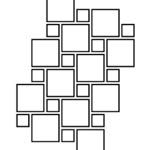
When we start with a simple tiling consisting of large and small square tiles (Figure 1), we can construct the latticework of mortar-joints by just removing the tiles. We will call this the tiling-lattice. The first step to make the tiling-lattice visible is to thicken the joints (Figure 2).
We then notice that apart from studying the tiling-lattice as a whole, there are a few basic new configurations we can make from it. First, the lattice can be seen as a set of contour lines (Figure 3). With this set we can, for example, make constructions by extending each contour and even interweave some contours. We can find an example of this in Escher's work: the entwined circular rings in his print Snakes (1969). Another possibility is to dismantle the lattice into equal-length bars, where each bar is a straight segment that is made up of a connected set of joints. The bar grids you then get can be used in 3-dimensional constructions in which bars overlap (Figure 4). Leonardo da Vinci was evidently interested in such bar constructions. In his work, I found drawings of three different regular bar grids [6, p. 154-155], and Figure 4 is one of them. We will discuss these and other possibilities of constructions with lattices at greater length in what follows.
First constructions with tiling lattices
Since the tiling-lattice is the net that remains after the tiles are removed, instead of tiles there are now holes. This means that we can overlay and interweave tiling-lattices. For example, in Figure 5, two copies of the lattice in Figure 2 have been interwoven. We have already noticed that from the drawing of contours (as in Figure 3), connected constructions also can be made by extending the contours.
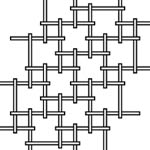

Figure 4
Figure 5