 |
 |
 |
 |
 |
 |
 |
|
|
 |
|
|
|
 |
|
The Elevation of Coxeter’s Infinite Regular Polyhedron 444444
Abstract
In their book “La Divina Proportione” [1],[2], Luca Pacioli and Leonardo da Vinci described and illustrated an operation which you can apply to a polyhedron, called Elevation. Starting from Pacioli’s basic idea, resulting in a second layer around a polyhedral shape, we can develop this idea further towards entwined double layer structures. Some of them are single objects, others appear to be compounds.
1. Introduction
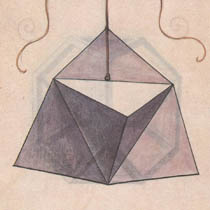
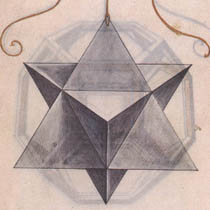
1.1. La Divina Proportione. In their book “La Divina Proportione”, published in 1509, Luca Pacioli and Leonardo da Vinci introduced the concept of Elevation, an operation that could be applied on the Platonic polyhedra as well as on the Archimedean polyhedra. The elevated versions of the first two Platonic solids, the tetrahedron and the octahedron, as they are drawn by Leonardo da Vinci, are shown in Figure 1 and 2.
|
|
|
|
 |
|
|
 |
|
 |
|
 |
|
|
|
Figure 1: Elevated Tetrahedron.
|
Figure 2: Elevated Octahedron.
|
Figure 3: Pacioli’s description.
|
|
| 1.2. Elevation. To understand what Elevation means we have to go to “La Divina Proportione” [3], chapter L, paragraph XIX.XX, where Pacioli describes the elevated version of the octahedron as follows: “And this object is built with 8 three-sided pyramids, that can be seen with your eyes, and an octahedron inside, which you can only see by imagination.”. This means that the object is composed of 32 equilateral triangular faces of which 8 are hidden (Figure 3). Pacioli describes the process of elevation as putting pyramids, built with equilateral triangles, but without the bottom faces, on each of the faces of the polyhedra. The result of this operation is a double layered object and has many similarities with the stellated version of the octahedron. However “stellation” was introduced about a century later by Johannes Kepler in his “Hamonices Mundi” (1619). Kepler defined stellation for polyhedra, as the process of extending faces until they meet to form a new polyhedron. That means that the stellation of the octahedron consists of eight faces, just as the octahedron itself, instead of the 32 faces mentioned by Pacioli. Also the number of vertices is different: the stellation of the octahedron has 6 vertices (again the same number as the octahedron itself) whereas the elevated octahedron has 14 vertices (6 of the octahedron + 8 of the pyramids). |
|
|
| 1.3. Vertex Figure. Let us have a closer look at the elevated octahedron (Figure 4). And especially at the 6 vertices of the original octahedron. After adding the 8 three-sided pyramids at each of the faces, we now have 12 triangles coming together in each of these vertices. Normally, in a polyhedron, just two faces join along any common edge. In the elevation however we have some edges where four faces come together. By the way Pacioli describes the process of elevation, it is very clear which faces are really joined. So when we look at the vertex figure around one of those vertices (the figure that we get when we “walk” around the vertex), we see that we have a first loop on the outer shell of the elevation (Figure 5), and a second loop on the inner shell (on the octahedron that is still inside), Figure 6. So the connection of the faces in these vertices can be described as follows: 33333333 (the faces of 4 pyramids surrounding a vertex) plus 3333 (the faces of the octahedron). |
|
 |
|
 |
|
 |
|
|
|
Figure 4: Elevated Octahedron.
|
Figure 5: Elevated Octahedron.
|
Figure 6: Composition.
|
|
| 1.4. Elevation Element. Because of the special situation that four faces come together at each of the edges that meet in these vertices, we can take an alternative choice in pairing the faces. For instance, we can start our walk around the vertex on one of the faces of the octahedron and then step to an adjacent face of a three-sided pyramid |
|
|
 |
|
 |
|
 |
|
|
|
Figure 7: Alternative loops.
|
Figure 8: Stella Octangula.
|
Figure 9: Elevation element.
|
|
| When we continue our walk, we can make a loop-like the blue line in Figure 7. Again we end up with two loops around the vertex, but now the two loops are interlinked and the elevation splits up in two tetrahedron-like figures instead of one octahedron plus eight three-sided pyramids. It comes close to Kepler’s stellated octahedron (Figure 8), but there is still a difference: we don’t have real tetrahedra because the big triangles are in fact four joined triangles. Let us define this set of joined faces, one face of the basic polyhedron (in this case the octahedron) surrounded by faces of the elevation pyramids, one at each of the edges, as the “elevation element” (Figure 9). |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|








